O problema do caxeiro viajante pode ser resolvido

Uma matemático da HP, chamado Vinay Deolalikar distribuiu cópias de um artigo preliminar intitulado de “P =/= NP”. Se esse cara realmente conseguiu resolver P X NP de forma não exponencial, isto poderá trazer resoluções para diversos problemas computacionais como o caso do caxeiro viajante (link para versão explicada no Wikipedia).

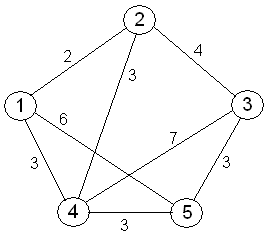O problema do caixeiro-viajante (figura ao lado) consiste na procura de um circuito que possua a menor distância, começando numa qualquer cidade, entre várias, visitando cada cidade precisamente uma vez e regressando à cidade inicial.

O tamanho do espaço de procura aumenta exponencialmente dependendo de n, o número de cidades, uma vez que existem:

O problema do caixeiro-viajante é enfrentado rotineiramente pela indústria. Na fabricação de chips, por exemplo, as empresas buscam encontrar uma rotina que minimize o número de movimentos de um braço robótico, a fim de economizar tempo e energia.

Para termos idéia da dimensão e de quanto é importante esta resolução, existe um prêmio de US$ 1 milhão de dolares par quem apresentasse  uma resolução, oferecida pelo Instituto Clay de Matemática. Ainda é uma primeira versão, mas teóricos de complexidade receberam bem o artigo de Dolalikar. Mas, quando a versão final for divulgada na semana que vem, o processo de avaliação deverá ser intensificado.

Para quem quiser ir um pouco além, é interessante começar pelo entendimento de complexibilidade de algorítimos, link: http://pt.wikipedia.org/wiki/Complexidade_computacional

A notícia foi dada na Folha